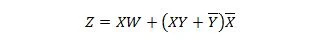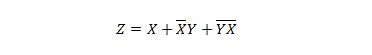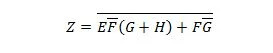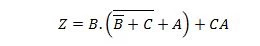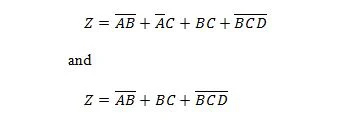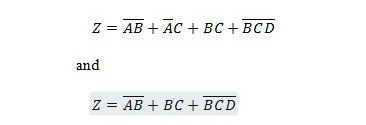Глава 2: Булева алгебра и связанные с ней компьютерные компоненты

Глава 2: Булева алгебра и связанные с ней компьютерные компоненты

2.1 Основные логические операторы

Предположим, что я (автор) высокий, а вы (читатель) высокие. Если кто-то спросит вас, высокие ли мы оба, вы ответите «Да» (правда). Если он спросит, низкий ли у нас обоих рост, вы ответите «Нет» (ложь). Если вы невысокого роста, а я высокий, и он спрашивает вас, высокий ли вы или я, ваш ответ будет «Да» (правда). Если он спросит, высокие ли мы с тобой, у тебя не будет ответа. Далее вы можете сказать, что последний вопрос не следует задавать или что на этот вопрос нет ответа. Что ж, я хочу, чтобы вы (читатель) знали, что сегодня при определенных обстоятельствах следует задать этот вопрос.

В биологии человек либо высокий, либо низкий. Именно «средовые» условия обуславливают наличие у человека среднего роста. Один учёный, Джордж Буль, определил набор ответов или правил для такого рода вопросов. Мы изучим эти правила в этом разделе онлайн-курса карьеры (глава). Эти правила сегодня используются в вычислительной технике, программировании, электронике и телекоммуникациях. Фактически, без этих правил у вас не было бы компьютера, как это принято сегодня; у вас также не было бы программирования, как это принято сегодня.

Правда или ложь
Простое высказывание на человеческом языке само по себе либо истинно, либо ложно. Если я говорю: «Я высокий», это либо правда, либо ложь. Если я скажу: «Ты высокий», это либо правда, либо ложь. Если я высокий, а вы невысокий, и задается вопрос, высокие ли мы с вами, в булевой логике должен быть дан ответ «истина» или «ложь». Что из этих двух следует подарить? Буль толком не ответил на этот вопрос. Он просто придумал набор правил, которым мы должны следовать. Хорошая новость заключается в том, что если вы будете следовать этим правилам в правильном контексте, у вас не возникнет никакой двусмысленности. Благодаря этим правилам сегодня у нас есть компьютеры и программирование. Правила даны вам сейчас. Правила невозможно объяснить; вы просто принимаете их. Правила разделены на три заголовка: И, ИЛИ и НЕ.

И
Вопрос можно задать, если и ты, и я высокие. Затем мой рост и ваш рост объединяются по набору правил AND. Это правила AND, которым необходимо следовать:

ложь И ложь = ложь
ложь И истина = ложь
истина И ложь = ложь
истина И истина = истина

Теперь пусть высокое будет истинным, а короткое — ложным. Это означает, что если я невысокого роста И вы невысокого роста, то мы с вами невысокие. Если я невысокий, а ты высокий, мы с тобой низкие; это логический ответ, который вы должны принять. Если я высокий, а ты невысокий, то мы с тобой низкие. Если я высокий И ты высокий, мы с тобой высокие. Все это И логические правила, которые вы (читатель) просто должны принять.

ИЛИ
Вопрос можно задать, если вы ИЛИ я высокий. Затем мой рост и ваш рост объединяются в соответствии с набором правил OR. Вот правила ИЛИ, которым следует следовать:

ложь ИЛИ ложь = ложь
ложь ИЛИ правда = правда
истина ИЛИ ложь = истина
истина ИЛИ истина = истина

Опять же, пусть высокое будет истинным, а короткое — ложным. Это означает, что если у меня низкий рост ИЛИ у вас низкий рост, то у вас ИЛИ у меня низкий рост. Если я невысокого роста ИЛИ вы высокий, то вы или я высокие. Если я высокий ИЛИ ты невысокого роста, то ты ИЛИ я высокий. Если я высокий ИЛИ вы высокий, то вы или я высокий. Все это логические правила, которые вам придется принять.

НЕТ
Теперь в булевой логике существуют только два состояния (возможных ответа). То есть, если ты НЕ высокий, ты низкий. Если вы НЕ невысокого роста, вы высокий; ничего больше. Вот правила НЕ, которым следует следовать:

НЕ ложь = правда
НЕ правда = ложь

Предположим, что у вас есть веревка (или пружина), которую вы можете растянуть (потянуть). Пока строка находится в своем естественном состоянии, если я скажу «НЕ короткая», вы ее расширите; это интерпретация. Пока строка растянута, если я скажу «НЕ длинная», вы позволите ей сжаться; это интерпретация.

Вам необходимо запомнить все данные правила в разных категориях.

Более двух операндов
В компьютерном языке И, ИЛИ и НЕ называются операторами. Для оператора NOT вам нужен только один операнд (значение оператора), чтобы получить ответ. Для операторов AND или OR вы можете иметь более двух операндов. В предыдущих случаях показаны два операнда: И и ИЛИ. У вас может быть три операнда для AND следующим образом:

ложь И ложь И ложь = ложь
ложь И ложь И истина = ложь

Это две строки; каждый имеет два оператора AND. На самом деле строк девять, когда операндов три. При использовании оператора AND только последняя строка (девятая строка) равна true; все предыдущие строки ложны. Обратите внимание, что при наличии двух операндов для AND только последняя строка остается истинной; все предыдущие три строки ложны. Когда операндов четыре, строк 16, и только последняя строка верна для оператора AND.

Шаблоны для AND и шаблоны для OR различны. С тремя операндами для двух операторов ИЛИ также имеется девять строк, и только первая строка на этот раз является ложной. Со второй по девятую строки верно. Обратите внимание, что при наличии двух операндов для ИЛИ только первая строка остается истинной; все остальные три строки ложны. Если операндов для ИЛИ четыре, строк также будет 16.

Оператор NOT имеет дело только с одним операндом. НЕ ложь — истина, а НЕ истина — ложь.

2.2 Таблица истинности двух операндов и их электронные компоненты

В математике есть такая тема, как алгебра. Небольшую часть этого мы видели в предыдущей главе. Существует разновидность алгебры, называемая Булевой алгеброй. В булевой алгебре истинность определяется по двум базисным цифрам, равным 1, а ложь определяется по двум базисным цифрам, равным 0.

Внутренние компоненты компьютерного блока являются электронными компонентами. Системный блок компьютерной системы имеет цифровые электронные компоненты. Операция И выполняется небольшим электронным компонентом, называемым вентилем И. Операцию ИЛИ выполняет небольшой электронный компонент, называемый вентилем ИЛИ. Операция НЕ выполняется небольшим электронным компонентом, называемым вентилем НЕ. Слишком много таких вентилей может находиться в микросхеме интегральной схемы (ИС).

И Таблица истинности и ее ворота
В следующей таблице представлена ​​таблица истинности И и ее символ логического элемента И (маленькая схема):

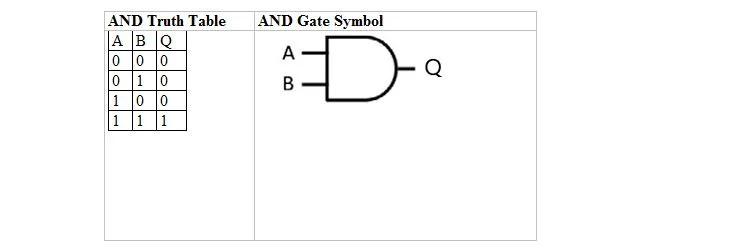
И для таблицы истинности AND, и для ее вентиля A и B являются двумя входными переменными. Q — выходная переменная. A равно 1 или 0. B равно 1 или 0. Q равно 1 или 0. Таблица истинности И с 1 и 0 аналогична предыдущей схеме истинности Истина/ложь И (таблица). Уравнение И:

А. Б = К

где точка (.) означает И (логическое значение). Точку можно опустить, чтобы AB = Q, что означает то же самое (И).

Примечание. Биты A и B в четырех строках в виде пар представляют собой первые четыре числа по второму основанию, начиная с 0 (или 00), т. е. 00, 01, 10, 11.

В следующей таблице представлена ​​таблица истинности ИЛИ и ее символ вентиля ИЛИ (маленькая схема):

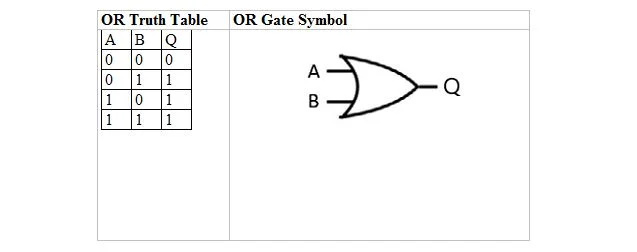
И для таблицы истинности ИЛИ, и для ее вентиля A и B являются двумя входными переменными. Q — выходная переменная. Таблица истинности ИЛИ с 1 и 0 аналогична предыдущей схеме истинности ИЛИ (таблица).

Уравнение ИЛИ:

А + Б = Q

Здесь + означает логическое ИЛИ, а не сложение. Уравнение читается как «A или B равно Q».

В следующей таблице представлена ​​таблица истинности НЕ и ее символ НЕ-вентиля (маленькая схема):

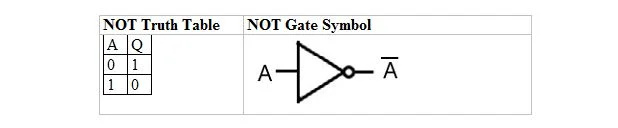
Таблица истинности НЕ или вентиль НЕ имеет только один вход и один выход. Когда входной сигнал равен 0, выходной сигнал равен 1. Когда входной сигнал равен 1, выходной сигнал равен 0. Логический элемент НЕ выполняет своего рода инверсию. Выходная переменная такая же, как и входная, но с чертой (перечеркнутой). Таблица истинности НЕ с 1 и 0 аналогична предыдущей схеме истинности ИЛИ (таблица).

Уравнение НЕ:

А = К

Где Q = A и черта над A здесь означает дополнение. Дополнение 0 равно 1, а дополнение 1 равно 0. Вентиль НЕ также известен как вентиль ИНВЕРТИРУЮЩИЙ.

Это фундаментальные (или корневые) таблицы истинности и их вентили (маленькие схемы) в цифровой электронике (с булевой алгеброй). Остальные три таблицы истинности, приведенные на следующем рисунке, и их элементы созданы для удобства и основаны на трех предыдущих таблицах истинности.

Существует таблица истинности и вентиль, которые являются производными от таблицы и вентиля И. Они называются таблицей истинности И-НЕ (от НЕ-И) и соответствующим вентилем И-НЕ. Таблица истинности NAND и ее вентиль NAND:

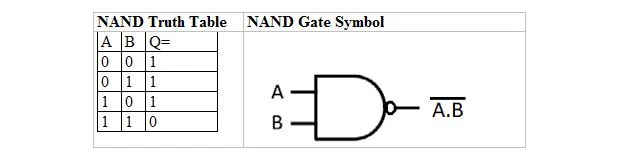
Чтобы получить таблицу истинности И-НЕ, перейдите к выводу таблицы истинности И и замените каждую цифру ее дополнением. Дополнение 0 равно 1, а дополнение 1 равно 0. Вентиль И-НЕ похож на вентиль И, но перед выходной линией имеет небольшой кружок. Уравнение И-НЕ:

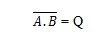
Где означает дополнение результата «А» И «Б». Перекладина (над линией) представлена ​​в воротах маленьким кружком. Обратите внимание, что точку между A и B можно опустить.

Существует еще одна таблица истинности и вентиль, которые являются производными от таблицы и вентиля истинности ИЛИ. Они называются таблицей истинности NOR (от NOT OR) и соответствующим вентилем NOR. Таблица истинности NOR и ее ворота NOR:

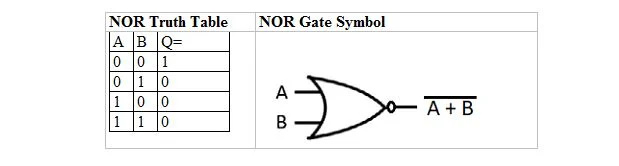
Чтобы получить таблицу истинности ИЛИ, перейдите к выводу таблицы истинности ИЛИ и замените каждую цифру ее дополнением. Дополнение 0 равно 1, а дополнение 1 равно 0. Вентиль ИЛИ похож на вентиль ИЛИ, но перед выходной линией имеет небольшой кружок. Уравнение NOR:

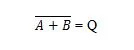
Где 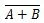означает дополнение результата «A» ИЛИ «B». Полоса (верхняя линия) представлена ​​в воротах маленьким кружком.

Исключающее ИЛИ (XOR)
Таблица истинности для вентиля ИЛИ:

В обычном английском языке неясно, должна ли последняя строка 1 OR 1 давать 1 или 0. Итак, в булевой алгебре существует два типа таблиц истинности ИЛИ и два соответствующих вентиля. При обычном ИЛИ последняя строка 1 ИЛИ 1 дает 1. Другой тип ИЛИ — исключающее ИЛИ (XOR), где первые три строки такие же, как первые три строки обычного ИЛИ (включая выходные данные). Однако для четвертой и последней строки 1 ИЛИ 1 дает 0.

В следующей таблице представлена ​​таблица истинности исключающего ИЛИ и символ ее элемента исключающее ИЛИ (маленькая схема):

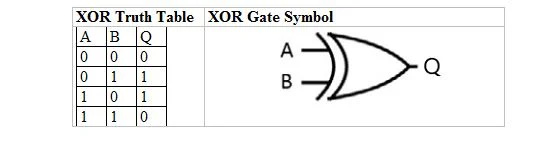
Как для таблицы истинности XOR, так и для ее вентиля «A» и «B» являются двумя входными переменными. «Q» — выходная переменная.

Уравнение XOR:

А ⊕ Б = Q

Здесь ⊕ означает логическое исключающее ИЛИ.

Обычное ИЛИ означает одно или оба. Эксклюзивное ИЛИ означает строго или и не то и другое.

2.3 Булевы постулаты

Постулаты – это предположения, на основе которых делаются определенные выводы. Существует десять логических постулатов, основанных на уравнениях И, ИЛИ и НЕ (таблицах истинности). Эти уравнения еще называют функциями. Основные функции копируются следующим образом:

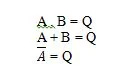
Это фундаментальные функции (уравнения) булевой алгебры. Следующие три других (функциональных) уравнения не являются фундаментальными функциями:

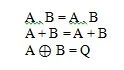
Последняя функция здесь хоть и своеобразна, но не считается фундаментальной.

Булевы постулаты заключаются в следующем:

Из функции И
1) 0 . 0 = 0
двадцать . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1

Из функции ИЛИ
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1

Из функции НЕ
9) 0 = 1
10) 1 = 0

Примечание: Эти постулаты представляют собой всего лишь строки в таблицах истинности И, ИЛИ и НЕ, выраженные независимым образом. Читателю следует запомнить данные постулаты.

2.4 Логические свойства

Свойство – это подобие характеристики чего-либо. Булевы свойства — это уравнения, выведенные из булевых постулатов. В этом разделе свойства просто задаются без их производных, а затем используются впоследствии. Есть двадцать пять объектов недвижимости, которые сгруппированы под десятью заголовками следующим образом:

Свойства функции И

Свойство 1:

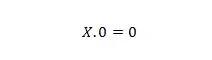
Где X может быть 1 или 0. Это означает, что независимо от того, что такое X, результат всегда равен 0.

Примечание. Переменная не обязательно должна быть A, B, C или D. Переменная может быть W, X, Y, Z или любой другой буквой.

Свойство 2:

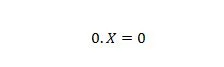
Где X может быть 1 или 0. Обратите внимание, что разница между свойством 1 и свойством 2 заключается в том, что в левой части знака равенства обоих уравнений позиции X и 0 меняются местами.

Свойство 3:

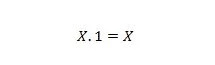
Если X равен 0, то 0. 1 = 0. Если X равен 1, то 1. 1 = 1.

Свойство 4:

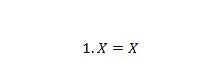
Если X равно 0, то 1. 0 = 0. Если X равно 1, то 1. 1 = 1. Обратите внимание, что разница между свойством 3 и свойством 4 состоит в том, что в левой части обоих уравнений позиции X и 1 поменяны местами.

Свойства функции ИЛИ

Свойство 5:

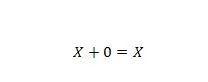
Где X может быть 1 или 0. Это означает, что если X равен 0, результат равен 0. Если X равен 1, результат равен 1.

Свойство 6:

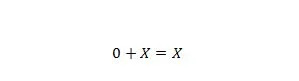
Где X может быть 1 или 0. Обратите внимание, что разница между свойством 5 и свойством 6 заключается в том, что в левой части обоих уравнений позиции X и 0 меняются местами.

Свойство 7:

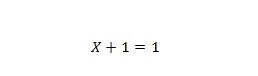
Если X равен 0, то 0 + 1 = 1. Если X равен 1, то 1 + 1 = 1.

Свойство 8:

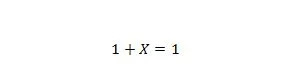
Если X равно 0, то 1 + 0 = 1. Если X равно 1, то 1 + 1 = 1. Обратите внимание, что разница между свойством 7 и свойством 8 состоит в том, что в левой части обоих уравнений позиции X и 1 поменяны местами.

Свойства, касающиеся комбинации переменной с самой собой или с ее дополнением

Свойство 9:

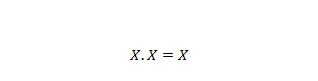
То есть: если X равен 0, то 0. 0 = 0. Если X равен 1, то 1. 1 = 1.

Свойство 10:

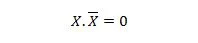
То есть: если X равен 0, то 0. 1 = 0. Если X равен 1, то 1. 0 = 0.

Для последовательных переменных это свойство принимает вид:

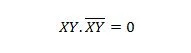
Свойство 11:

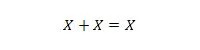
То есть: если X равен 0, то 0 + 0 = 0. Если X равен 1, то 1 + 1 = 1 (из обычного ИЛИ).

Свойство 12:

То есть: если X равен 0, то 0 + 1 = 1. Если X = 1, то 1 + 0 = 1.

То есть: если X равен 0, то 0 + 1 = 1. Если X = 1, то 1 + 0 = 1.

Двойное дополнение

Свойство 13:

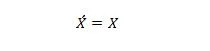
Когда X в левой части равно 0, X в правой части становится 0. Когда X в правой части равно 1, X в левой части становится 1. Другими словами, двойное дополнение возвращает исходное значение.

Коммутативный закон

Свойство 14:

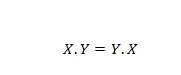
Это означает, что замена первого и второго операндов для оператора И слева от знака равенства не имеет значения; ответ остается тем же после того, как произошел обмен на левой стороне. Это уравнение можно записать без точек так: XY = YX.

Свойство 15:

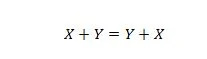
Объяснение здесь такое же, как и в предыдущем AND, но оно относится к оператору OR.

Распределительный закон

Свойство 16:

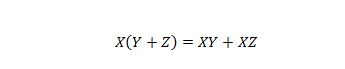
Здесь есть три переменные: X, Y и Z. Каждая переменная может иметь значение 1 или 0. Скобки слева от символа равенства означают, что в первую очередь нужно оценить то, что в них находится. Тогда AND — это результат с X. Правая часть говорит, что X И Y вместе, ИЛИ X И Z вместе, такие же, как и левая часть. Обратите внимание, что оператор точки для AND полностью опущен; и объединенные переменные по-прежнему означают И.

Свойство 17:

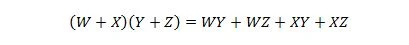
Это свойство является расширением свойства 16 с добавлением переменной W.

Ассоциативный закон

Свойство 18:

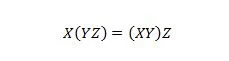
Скобки означают, что сначала нужно оценить то, что находится в скобках. Итак, для выражения в левой части, если Y с Z сначала соединяются И, а X объединяется с результатом, то окончательный результат в левой части будет таким же, как окончательный результат справа. -сторона, где X с Y сначала объединяется с помощью AND, а затем складывается AND с результатом с Z. Обратите внимание, что точки в уравнении опущены.

Свойство 19:

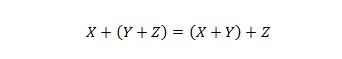
Это свойство объясняется аналогично свойству 18, но вместо оператора AND используется оператор OR. Для простоты оператор ИЛИ + никогда не опускается в логическом выражении. С другой стороны, оператор AND можно опустить и объединить две переменные.

Поглощение

Свойство 20:

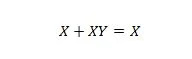
В этом уравнении, независимо от того, что такое Y, правая часть всегда будет X (поглощенной).

Свойство 21:

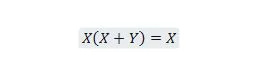
Кроме того, в этом уравнении, независимо от того, что такое Y, правая часть всегда будет X (поглощенной). Это свойство 21 такое же, как и свойство 20, которое:

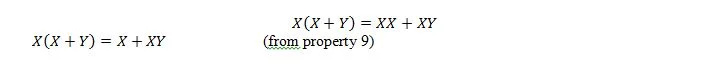
Здесь мы используем распределительный закон и тот факт, что X.X = X свойства 9.

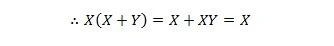
Личность

Свойство 22:

Это означает, что для выражения X + Y дополнение X перед Y не меняет выражение.

Свойство 23:

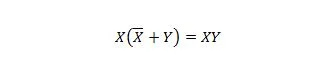
Это означает, что для выражения XY дополнение X по ИЛИ с Y в скобках, которое делается первым, не меняет выражение XY.

Закон ДеМоргана

Свойство 24:

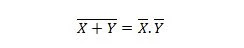
Это означает, что логический элемент ИЛИ (НЕ ИЛИ) имеет тот же результат, что и НЕТ двух входов перед их объединением И.

Свойство 25:

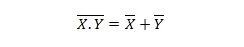
Это означает, что логический элемент И-НЕ (НЕ И) имеет тот же результат, что и НЕ-два входа перед операцией ИЛИ.

На иллюстрациях представлены 25 объектов недвижимости. Их можно доказать, подставив все возможные значения 1 и 0 в каждое выражение в левой части, чтобы увидеть, получено ли выражение (или результат) в правой части. Доказательства оставлены в качестве упражнения для читателя.

2.5 Упрощение сложных выражений

Следующие две функции одинаковы:

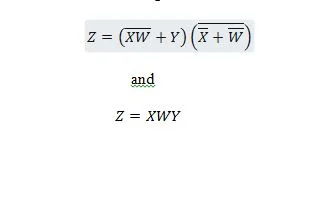
Z — это выход, а X, W и Y — входы. Первому нужны вентиль И-НЕ, вентиль ИЛИ, вентиль И, два вентиля НЕ, вентиль ИЛИ и вентиль ИЛИ. Второму нужно всего два вентиля И. Первое представляет собой уравнение с составным выражением в правой части, которое было упрощено (сведено) до единственного члена правого выражения для второго уравнения.

Упрощение или сокращение приводит к меньшему количеству вентилей для реализации той же функции, что и схема. Такая меньшая схема может быть частью интегральной схемы (ИС) или отдельной схемой на поверхности материнской платы компьютера.

Когда функция (уравнение) попадает в процесс проектирования, необходимо выполнить упрощение, чтобы уменьшить количество вентилей и в конечном итоге получить более дешевую схему. Упрощение требует использования одного или нескольких из предыдущих двадцати пяти логических свойств.

Пример 2.51:

Сократите уравнение:

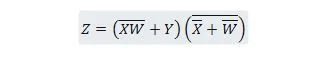
Примечание: Две круглые скобки рядом друг с другом означают, что скобки объединены оператором AND (точка между ними необязательно может быть прописана).

Решение:
Для решений обоснование (причина) каждого шага дается справа от шага, в скобках. Читателю следует прочитать каждый шаг и его обоснование. Читатель должен также обращаться к предыдущим свойствам, когда он/она читает шаги сокращения функции.

Пример 2.52:

Упрощать:

2.6 Минимальная сумма произведений

Следующие две функции одинаковы:

Говорят, что оба правых выражения обоих уравнений имеют форму суммы произведений (SP). Говорят, что экспресс-выражение находится в форме суммы произведения, если в нем нет круглых скобок. Очевидно, что первой функции (уравнению) требуется больше элементов, чем второй функции.

Первое правое выражение все еще можно сократить, чтобы получить вторую функцию. Второе выражение в правой части не может быть упрощено дальше и при этом может быть выражено как сумма произведений («добавление» членов). Второе выражение в правой части невозможно упростить дальше. Итак, говорят, что он находится в форме минимальной суммы произведений (MSP).

Пример 2.61:
Принесите следующую функцию сначала в форму «Сумма продуктов», а затем в форму «Минимальная сумма продуктов».

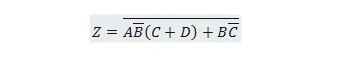
Решение:
При решении подобных задач необходимо использовать одно или несколько из предыдущих двадцати пяти свойств, как показано в этом решении:

2.6 Минимальная сумма произведений

Следующие две функции одинаковы:

Говорят, что оба правых выражения обоих уравнений имеют форму суммы произведений (SP). Говорят, что экспресс-выражение находится в форме суммы произведения, если в нем нет круглых скобок. Очевидно, что первой функции (уравнению) требуется больше элементов, чем второй функции.

Первое правое выражение все еще можно сократить, чтобы получить вторую функцию. Второе выражение в правой части не может быть упрощено дальше и при этом может быть выражено как сумма произведений («добавление» членов). Второе выражение в правой части невозможно упростить дальше. Итак, говорят, что он находится в форме минимальной суммы произведений (MSP).

Пример 2.61:
Принесите следующую функцию сначала в форму «Сумма продуктов», а затем в форму «Минимальная сумма продуктов».

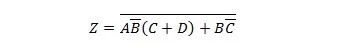
Решение:
При решении подобных задач необходимо использовать одно или несколько из предыдущих двадцати пяти свойств, как показано в этом решении:

Это последнее выражение представлено в форме суммы продуктов (SP), но не в форме минимальной суммы продуктов (MSP). На первую часть вопроса дан ответ. Решение второй части следующее:

Эта последняя упрощенная функция (уравнение) имеет форму MSP и требует меньшего количества вентилей для реализации, чем соответствующая ей форма SP. Помните: SP означает сумму продуктов, а MSP означает минимальную сумму продуктов.

Пример 2.62:
Следующая схема имеет входы X, Y и W, а Z — выход. Создайте функцию суммы продуктов (SP) (функцию кажущейся минимальной суммы продуктов) для Z. Затем создайте истинную, более уменьшенную (минимизированную) сумму продуктов (MSP). Затем реализуем схему MSP (нарисуем вентильную сеть MSP).

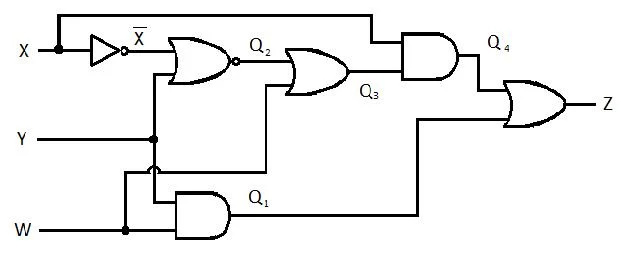
Рис. 2.61. Схема управления.

Решение:
Прежде чем начать процесс упрощения, выражение для Z должно быть получено через X, Y и W. См. пример иллюстрации на диаграмме:

Это выражение Z через X, Y и W. После этого может произойти упрощение до видимого MSP. Очевидный MSP — SP.

Это последнее уравнение (функция) имеет форму SP. Это неверно. Минимальная сумма продуктов (еще не MSP). Значит, сокращение (минимизацию) должно продолжаться.

Это последнее уравнение (функция) представляет собой истинную минимальную сумму произведений (MSP). И схема управления минимальной суммой произведений (истинное минимизация) равна:

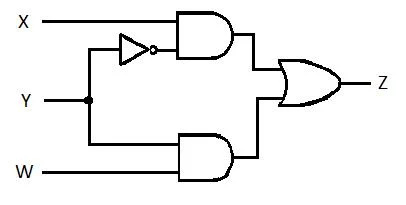
Рис. 2.62. Схема управления MSP.

Комментарий
Из анализа, приведенного в этом разделе, видно, что неясно, является ли сумма произведений минимальной суммой произведений или нет. SP не очень полезен. Именно MSP очень полезен. Существует надежный способ получить MSP; это использование карты Карно. Карта Карно выходит за рамки этого онлайн-курса карьеры.

2.7 Проблемы

Читателю рекомендуется решить все задачи в главе, прежде чем переходить к следующей главе.

1. Создайте таблицы истинности И, ИЛИ и НЕ с соответствующими вентилями.
2. Запишите десять логических постулатов по разным категориям, называя категории.
3. Без объяснения запишите двадцать шесть свойств булевой алгебры в различных категориях, называя категории.
4. Сократите уравнение, используя логические свойства и указывая используемые категории.



5. Сократите уравнение, используя логические свойства и указывая используемые категории.



6. Используя логические свойства и заключая в кавычки используемые категории, сократите следующее уравнение – сначала до суммы произведений, а затем до минимальной суммы произведений:



7. Используя логические свойства и заключая в кавычки используемые категории, сократите следующее уравнение – сначала до суммы произведений, а затем до минимальной суммы произведений: